二叉查找树定义
二叉查找树(英语:Binary Search Tree),也称二叉搜索树、有序二叉树(英语:ordered binary tree),排序二叉树(英语:sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
应用场景
二叉查找树基本操作的复杂度与树的高度成正比,即一颗高度为h的树上各操作的时间复杂度为O(h),而树的高度与树的平衡性有关,最好情况下对于一颗含n个节点的完全二叉树,操作的复杂度为O(lgn),但是在最坏情况下二叉树退化成线性链,操作复杂度为O(n)。由此可知,在实际使用时应尽量保证数据的随机性,以使树的高度不至于过大。但是在现实中并不总能保证二叉查找树是随机构造成的,所以就出现了一些二叉查找树的变形,例如AVL树、红黑树等自平衡二叉查找树,后面的文章会逐一分析这些树的特性和算法实现。二叉查找树作为其它各类自平衡二叉查找树的基础,值得好好研究一下。
实现
数据结构定义
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
| typedef int(*compare)(void*, void*); typedef void(*print)(void*); typedef struct binarySearchTree BST; typedef struct nodeTag node; struct nodeTag { node *parent; node *left; node *right; void *data; }; struct binarySearchTree { node *root; compare cmp; print prt; };
|
每个节点node对象包含parent、left、right,分别指向节点的父节点、左儿子和右儿子。如果某个儿子节点或者父节点不存在,则相应域的值为NULL。数据域data指向数据地址。
BST是二叉查找树的结构定义,记录了树的根节点指针以及两个函数指针。cmp用于定义数据大小的比较,prt用于调试时的打印输出。
插入数据
插入数据可以分为以下几种情况:
- 根节点为空,则创建根节点,插入完成;
- 当前节点非空,key值小于要插入的数据key值,设置当前节点为左儿子节点;
- 当前节点非空,key值大于要插入的数据key值,设置当前节点为右儿子节点;
- 当前节点非空,key值等于要插入的数据key值,根据查找二叉树的定义不能有重复的节点,返回插入失败。
重复2、3、4步,直到当前节点为空,这个位置即是我们要插入节点的地方。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59
| int insert(BST *tree, void *val) { node *nd = NULL; if (!tree || !val) { return -1; } nd = (node *)calloc(1, sizeof(node)); if (!nd) { return -1; } nd->data = val; if (!tree->root) { nd->parent = NULL; nd->left = NULL; nd->right = NULL; tree->root = nd; } else { int cmpResult = 0; node *pre = NULL, *cur = NULL; cur = tree->root; while (1) { pre = cur; cmpResult = (*tree->cmp)(nd->data, cur->data); if (0 == cmpResult) { return -1; } else if (cmpResult < 0) { cur = cur->left; if (!cur) { nd->parent = pre; pre->left = nd; break; } } else { cur = cur->right; if (!cur) { nd->parent = pre; pre->right = nd; break; } } } } return 0; }
|
查找
查找过程可以使用递归的方式来实现。该过程从树的根节点开始,对碰到的每个节点与val做比较。如果比较结果相等,则查找结束。如果节点key值小于val,则继续查找左子树。如果节点key值大于val则继续查找右子树。也可以使用非递归的方式实现查找,原理与递归方式是一样的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
| node* find(BST *tree, void *val) { return findNode(tree, tree->root, val); } node* findNode(BST *tree, node* root, void *val) { int cmpResult = 0; if (!tree || !root || !val) { return NULL; } cmpResult = (*tree->cmp)(root->data, val); if (cmpResult == 0) { return root; } else if (cmpResult < 0) { return findNode(tree, root->right, val); } else { return findNode(tree, root->left, val); } }
|
遍历
树的遍历,即不重复地访问树的所有节点。与线性数据结构不同的是,从树的根节点出发,可以有多种路径可供选择,所以树的遍历就有了多种方式。
- 深度优先遍历:沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。
- 前序遍历:先访问根节点,然后访问左子树,最后访问右子树;
- 中序遍历:先访问左子树,然后访问根节点,最后访问右子树;
- 后续遍历:先访问左子树,然后访问右子树,最后访问根节点。
- 广度优先遍历:从根节点开始,沿着树的宽度遍历树的节点。
下面给出中序遍历的递归实现。前序遍历和后续遍历的实现与中序遍历大体相同,只需调整根节点、左子树和右子树的访问顺序即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
| int inOrder(BST *tree, node *nd) { return inOrderDepth(tree, nd, 0); } int inOrderDepth(BST *tree, node *nd, int sp) { int i = 0; if (!tree || !nd) { return -1; } inOrderDepth(tree, nd->left, sp + 1); for (i ; i < sp; i++) { printf("----"); } (*tree->prt)(nd->data); inOrderDepth(tree, nd->right, sp + 1); return 0; }
|
inOrderDepth函数参数sp辅助记录当前节点的深度,打印树结构时更加直观:
1 2 3 4 5 6 7 8 9 10 11 12
| ------------0 --------1 ------------7 ----12 ------------13 --------14 36 --------57 ----72 ------------76 --------87 ------------89
|
广度优先遍历通常会使用队列来实现,首先将根节点放入队列中,然后从队列中取出第一个节点,同时把这个节点的子节点加入队列,重复从队列取节点的过程直到队列为空,则遍历完成。
删除
二叉查找树删除节点相对来说较前面的插入、遍历等操作要复杂一些,因为删除节点不能破坏整棵树的结构,也就是说要保证删除节点之后依然是一颗二叉查找树。可以分为四种情况处理(nd为待删除的节点):
- nd为叶子节点:最简单的情况,修改父节点的left或right指针(nd为左儿子修改left指针,nd为右儿子修改right指针)为
NULL即可;
- nd左子树不为空、右子树为空:修改nd的左子树为nd父节点的左子树;
- nd右子树不为空、左子树为空:修改nd的右子树为nd父节点的右子树;
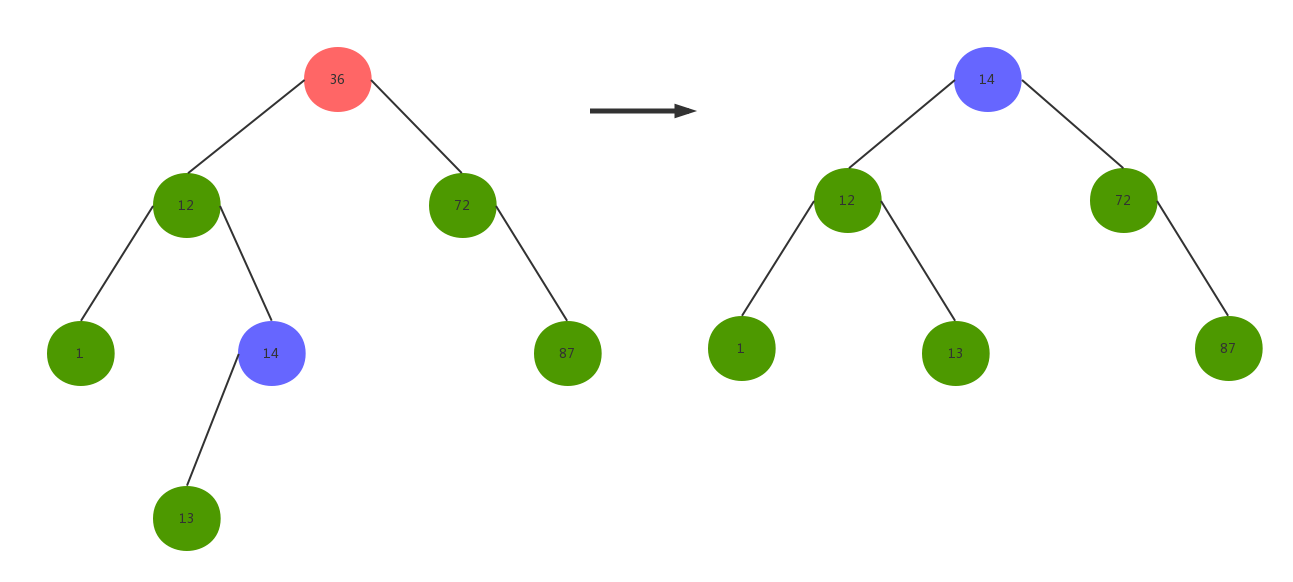
- nd左右子树都不为空:令nd的直接前驱(即nd左子树中最大的节点)或直接后继(即右子树中最小的节点)替代nd,然后再从二叉查找树中删去它的直接前驱(或直接后继)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92
| int del(BST *tree, void *val) { node *nd = NULL; if (!tree || !val) { return -1; } nd = find(tree, val); if (nd) { node *q, *s; if (!nd->left && !nd->right) { if (nd->parent) { if (nd->parent->left == nd) { nd->parent->left = NULL; } else { nd->parent->right = NULL; } } free(nd); nd = NULL; } else if (!nd->right) { q = nd->left; nd->data = q->data; nd->left = q->left; nd->right = q->right; if (q->left) { q->left->parent = nd; } if (q->right) { q->right->parent = nd; } free(q); q = NULL; } else if (!nd->left) { q = nd->right; nd->data = q->data; nd->left = q->left; nd->right = q->right; if (q->left) { q->left->parent = nd; } if (q->right) { q->right->parent = nd; } } else { s = nd; q = nd->left; while (q->right) { s = q; q = q->right; } nd->data = q->data; if (s != nd) { s->right = q->left; } else { s->left = q->left; } if (q->left) { q->left->parent = s; } free(q); q = NULL; } } return 0; }
|
完整代码:https://github.com/7byte/AlgorithmPractice/tree/master/%E6%A0%91

